空間とオイラーの公式／虚数についての考察


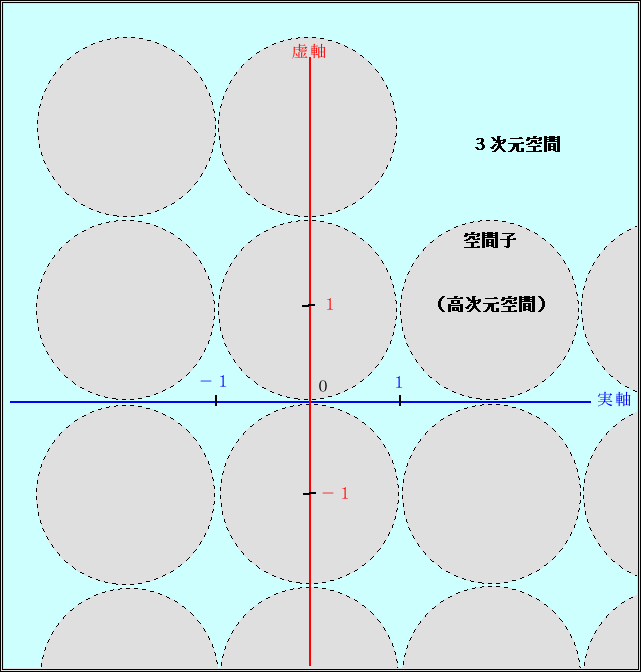
　３次元空間は、３次元球面（非常にコンパクトで極小）の集まりである。
　３次元空間を構成するこの３次元球面を「空間子（空間の構成要素）」と呼ぶこととする（複数種）。

　「空間子」を半径「１」の球と仮定すると、
　オイラーの公式　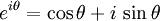　は、
　空間子の表面（球面）のある１点を中心とし、空間子の中心を通る半径「１」の円を表す。


　虚数単位「ｉ」は、「空間子」の内部空間（高次元空間）を表す。

　この「空間子」が、「ヒッグス粒子」に対応する。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（参照）オイラーの公式
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　グリゴリー・ペレルマン
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ダークマターについての考察

　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　平成２０年　３月１５日作成
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　平成２０年　５月２８日公開



　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　www.tawaraya-saketen.co.jp